Spirale logarytmiczne są wszędzie

Spirale logarytmiczne to jeden z ulubionych kształtów w przyrodzie. Powtarza się w różnych skalach i sytuacjach – od kształtu galaktyk po ułożenie liści czy kwiatów.

Spirala logarytmiczna powtarza się w różnych skalach i sytuacjach. Każde z głównych ramion Drogi Mlecznej to spirala logarytmiczna o kącie 12 stopni. Ramiona cyklonów tropikalnych układają się w spiralę logarytmiczną. Muszle mięczaków w przekroju tworzą taką spiralę. Układa się w nią również trasa lotu, po której owad zbliża się do źródła światła, a także rozwijająca się paproć czy kwiat brokułu.

Również humbaki doceniają piękno matematyki, tworząc ze spiralnie ułożonych bąbelków powietrza “sieci” na ryby i kryl – piszę o tym w oddzielnym artykule.

Zbiór Mandelbrota to z kolei zbiór punktów, którego krawędź na płaszczyźnie tworzy charakterystyczny wzór – jeden z najsławniejszych fraktali.

Co to jest złota spirala i spirala Fibonacciego?

Szczególnym przypadkiem (przybliżeniem) spirali logarytmicznej jest tzw. złota spirala, której szerokość zwiększa się (lub zmniejsza) o 90° dokładnie φ razy (φ to właśnie “złota liczba”).

Złote spirale są samopowtarzalne – po powiększeniu ich kształt może być powtarzany w nieskończoność.

Wygląda to tak:

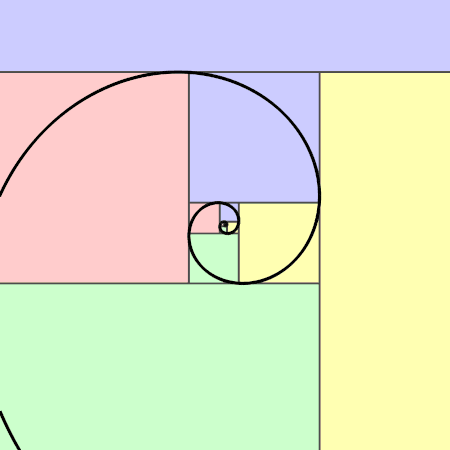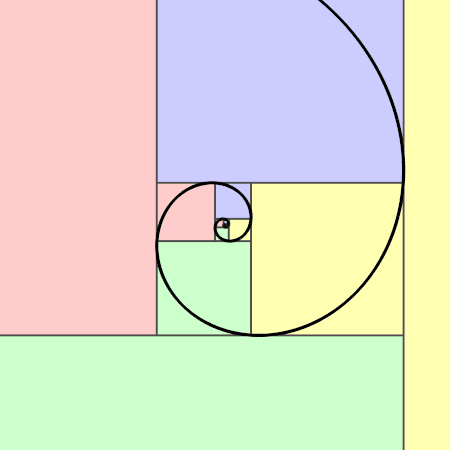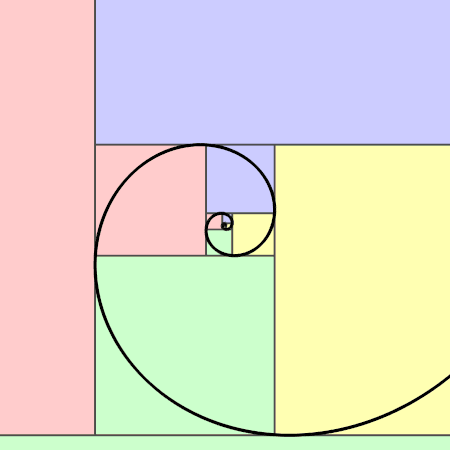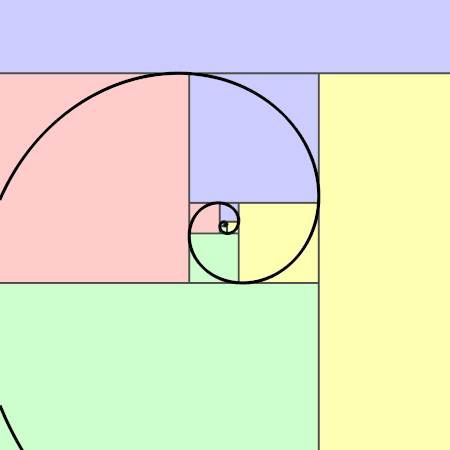
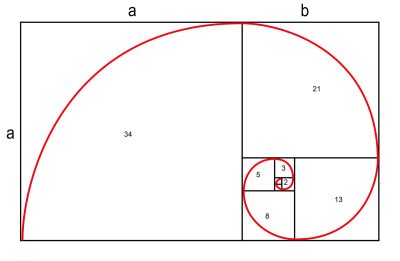
Z kolei spirala Fibonacciego jest przybliżeniem złotej spirali, ale nie złotą spiralą (choć bywa z nią mylona). Kiedy zobaczy się ją choć raz, to później dość łatwo jest intuicyjnie rozpoznać ją w przyrodzie.

Od strony matematycznej jest to rodzaj spirali zbudowanej z ćwiartek okręgów, których promienie są kolejnymi liczbami Fibonacciego. Z kolei ciąg Fibonacciego to ciąg liczb naturalnych określony rekurencyjnie w sposób następujący: pierwszy wyraz jest równy 0, drugi jest równy 1, każdy następny jest sumą dwóch poprzednich. Daje to następujący ciąg: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597… 

Spiralę Fibonacciego widuje się w kształtach wielu roślin, np. na owocu ananasa 8 linii spiralnych biegnie w jedną stronę, a 5 lub 13 w przeciwną, zaś na kwiatostanie słonecznika może się krzyżować 55 spiral z 89 (liczby te bywają większe). Spiralnie ułożone są różyczki kalafiora czy brokułu. 

Wynika to ze sposobu, w jaki rozwijają się organy takie jak łodyga, liście czy kwiaty. U większości roślin biorą one początek z centralnie usytuowanego skupiska komórek – merystemu. Każdy zawiązek kolejnego organu (liścia czy kwiatu) wyrasta z merystemu pod określonym kątem w stosunku do zawiązka, który pojawił się tam wcześniej.

Co fascynujące, u wielu roślin ten kąt jest taki sam i wynosi w przybliżeniu 137,5 stopnia! Jego dopełnienie do 360 stopni wynosi w przybliżeniu 5/8 kąta pełnego, w jeszcze większym przybliżeniu 8/13 kąta pełnego, jeszcze dokładniej 13/21 i tak dalej – jak widzicie, odzwierciedla to kolejne liczby z ciągu Fibonacciego. Ponieważ kątowi 137,5 stopnia nie odpowiada ściśle żaden ułamek zwykły, to nigdy nie dojdzie do tego, żeby kolejne zawiązki miały się rozwijać w tym samym kierunku. Dzięki temu organy roślin układają się w linie spiralne, a nie wyrastają z merystemu promieniście.