Dzięki tej książce stało się niemożliwe – polubiłam matematykę

Jestem jedną z tych osób, które matematyki w szkole nie lubiły i starały się jej w życiu wystrzegać. Aż do teraz. Bo matematyka mnie wreszcie dopadła – w książce „Pi razy drzwi”. I uwiodła mnie.

Moje „odkrycia” wydadzą się zapewne oczywiste tym spośród Was, którzy z matematyką mieli więcej do czynienia. Jednak to nie do nich jest przede wszystkim skierowana ta książka, tylko do tych, którzy matmę w szkole średniej uważali za zło konieczne i zrobili wszystko, żeby ustrzec się jej na studiach. Zupełnie jak ja. Kiedy więc dziewczyny z wydawnictwa Feeria Science zaczęły mnie namawiać do tego, żebym przeczytała książkę o matematyce, zjeżyłam się jak jeżozwierz. No, ale w końcu im to obiecałam, więc trzeba było chociaż spróbować. Ku mojemu OGROMNEMU zaskoczeniu wciągnął mnie już pierwszy rozdział, a potem było tylko lepiej. Serio!

Matematyka jest wokół nas, można znaleźć ją właściwie wszędzie bla bla bla… Mało przekonujące stwierdzenie? No to podam Wam kilka przykładów zaczerpniętych z „Pi razy drzwi, czyli dziwne przypadki matematyki”, tej cudotwórczej książki Mickaëla Launaya.

Na pierwszy ogień pójdzie ciąg Fibonacciego, który ujawnia się w naprawdę trudnych do uwierzenia okolicznościach. Chodzi o ciąg liczb odkryty przez Fibonacciego na podstawie prawidłowości… rozmnażania się królików. I tak na początku z jednej pary powstanie następna para młodych, potem z tej i poprzedniej pary urodzą się kolejne dwie pary… Ciąg ten wygląda następująco: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…

I co z tego?

To, że ku powszechnemu zaskoczeniu okazało się, iż ten charakterystyczny ciąg liczb świetnie oddaje sposób… układania się liści, kwiatów lub nasion wzdłuż głównej osi.

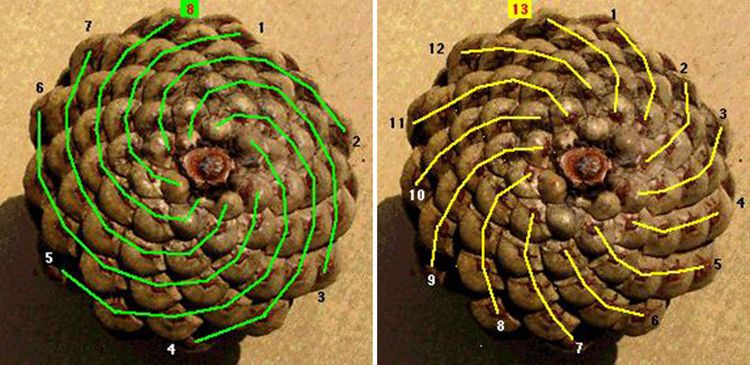
Szyszka: 8 i 13 spiral

Widać to dobrze w sosnowej szyszce, która na zewnątrz jest zbudowana ze spiralnie ułożonych łusek. Część spiral układa się zgodnie z kierunkiem wskazówek zegara, cześć – w przeciwnym kierunku. I wiecie co? Okazuje się, że liczba spiral z jednej i drugiej kategorii ZAWSZE jest kolejnymi elementami ciągu Fibonacciego!

To samo dotyczy elementów owocu ananasa, ułożenia ziaren w słoneczniku czy kwiatostanów w kalafiorze i brokułach. Przyroda jest pod tym względem bardzo konsekwentna.

Bryły, które bardzo chcą być sferami

W matematyce jest znacznie więcej takich niezwykłych, wręcz trudnych do uwierzenia prawidłowości. Weźcie do ręki piłkę do futbolu – taką klasyczną czarno-białą. Złożona jest z wyciętych ze skóry 20 białych sześcioboków i 12 czarnych pięcioboków. Dlaczego akurat takie zestawienie? To nie przypadek!

Kształt piłki wywodzi się od dwudziestościanu, jednej z brył platońskich, a więc takich, w których wszystkie ściany i kąty są jednakowe (łącznie jest tylko pięć brył platońskich). Dwudziestościan jest dość mocno kanciasty (składa się przecież z trójkątów), a w przypadku piłki, jak sami rozumiecie, przydałoby się, żeby jednak możliwie blisko przypominała sferę. Można ją do sfery upodobnić, „odkrawając” wystające wierzchołki dwudziestościanu, których jest 12. I właśnie po ich odcięciu pozostaną owe tajemnicze pięcioboki – tradycyjnie są one robione z czarnych kawałków skóry.

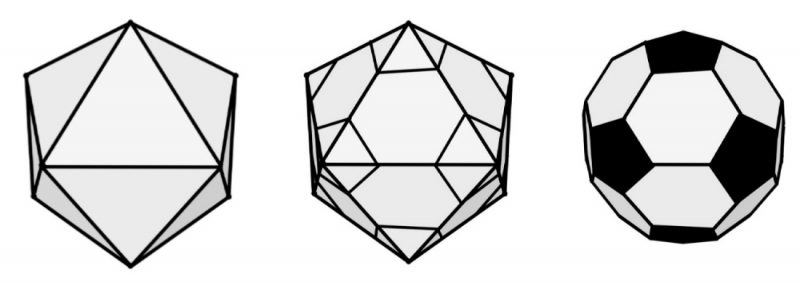
Dwudziestościan przekształcany w piłkę. Źródło: “Pi razy drzwi”

Że to niby nic wielkiego? Wcale nie, bo zasada 12 punktów stosuje się do wszystkich wielościanów mających pretensje do bycia foremnymi, ale nie są – takich, które „nadmuchujemy”, by zrobiły się większe. Tak jest w przypadku geody (czyli wielościanu o trójkątnych ścianach), w której – bez względu na to, czy jest wielka jak muszla koncertowa, czy też mała jak piłka – możemy znaleźć dokładnie 12 punktów odbiegających od reguł przyjętych w tej bryle. Odbiegających od reguł na podobnej zasadzie, na jakiej od reguł odbiega 12 czarnych łat na piłce.

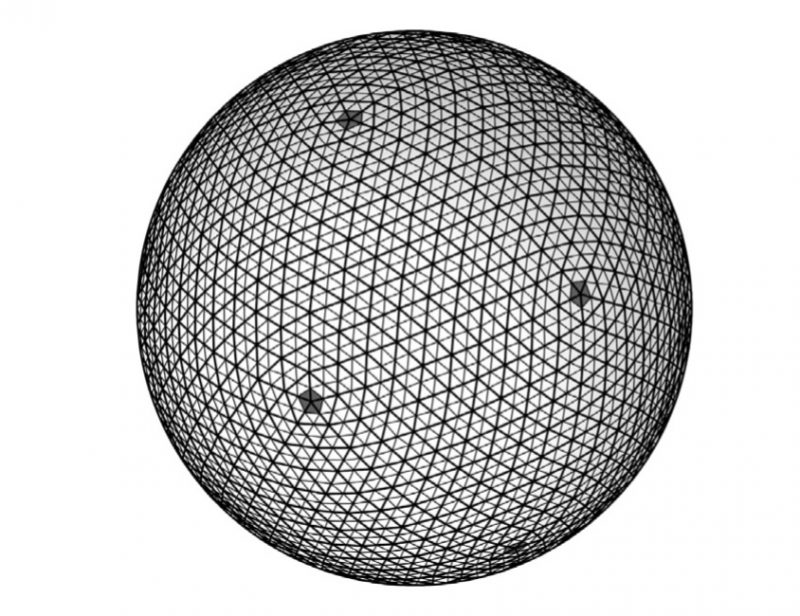
Płaskie odwzorowanie Geody i jej tysięcy trójkątów. Miejsca, w których trójkąty grupują się po pięć, zaznaczono ciemnoszarym odcieniem. Źródło: “Pi razy drzwi”

W geodzie w tych 12 niezwykłych punktach spotyka się nie sześć trójkątów (co jest w tej bryle regułą), tylko pięć trójkątów. Tych 12 nieregularności po prostu odpowiada 12 wierzchołkom wyjściowego dwudziestościanu, który poprzez podział trójkątów na coraz mniejsze “nadmuchano” tak, by jak najbardziej przypominał sferę. „Innymi słowy, są to te same miejsca, w których spotykają się wielkie trójkąty wyjściowej figury, po pięć w każdym wierzchołku dwudziestościanu. Owe wierzchołki, ostre na początku, zostają spłaszczone w procesie zwielokrotniania ścian i stają się niemal niezauważalne. Mimo to pozostają zakotwiczone w układzie trójkątów i uważni obserwatorzy mogą dostrzec tych 12 wciąż istniejących nieregularności” – pisze Mickaël Launay. Czyż to nie genialne w swej prostocie?

7 kategorii fryzów

I kolejna fascynująca prawidłowość, tym razem do obejrzenia na wszystkich wazach od Mezopotamii, przez Babilon i Grecję po Rzym. Chodzi o widoczne na nich geometryczne fryzy, czyli ozdobne pasy obiegające brzegi naczyń, wstęgi powstałe z użyciem jednego prostego motywu, który wielokrotnie powtarza się wzdłuż obwodu wazy. Wystarczy pójść do muzeum, żeby stwierdzić, iż starożytni twórcy wymyślili tak wielką mnogość fryzów, że gdyby chcieć je jakoś skategoryzować, to nie starczyłoby na to życia. Czy rzeczywiście?

Okazuje się, że geometria mocno trzyma w ryzach bogactwo fryzów. Nie, żeby ograniczało to twórców, ale bez względu na to, jaką fantazją by się wykazali, to i tak spod ich ręki wyjść musi taki wzór, który da się zaliczyć do którejś z zaledwie siedmiu możliwych kategorii! Jakakolwiek inna kombinacja jest geometrycznie NIEMOŻLIWA. Niesamowite!

Fot. Patrick Hoesly/Wikimedia

A wiecie, że podobne ograniczenia dotyczą również parkietaży? Parkietaże to takie „nadmuchane” fryzy, które zajmują całą płaszczyznę np. podłogi. Matematycy udowodnili, że „istnieje dokładnie ich 17 geometrycznych kategorii, które odpowiadają przekształceniom geometrycznym, względem których są niezmiennicze – pisze Mickaël Launay. – W każdej z tych kategorii może istnieć nieskończona liczba różnych wariantów. Arabscy artyści, nie znając tego twierdzenia, odkryli wszystkich siedemnaście i po mistrzowsku wpletli je w architekturę, w dzieła sztuki oraz w przedmioty codziennego użytku”.

Jeśli chcecie zobaczyć wszystkie 17 kategorii parkietaży, wybierzcie się do pałacu Alhambra w andaluzyjskiej Grenadzie, gdzie matematycy wpletli je w amfilady komnat i ogrodów.

A jeśli chcecie dać się uwieść matematyce, to przeczytajcie książkę Mickaëla Launaya. Jest ona fascynującą przechadzką po formowaniu się historycznych podstaw tej królowej nauk. Naprawdę warto!

Pi razy drzwi, czyli dziwne przypadki matematyki

Autor: Mickaël Launay

Wydawca: Feeria Science

2017